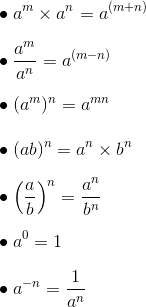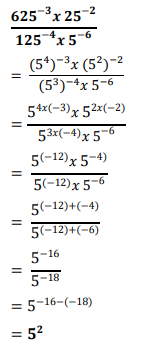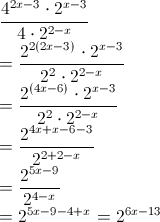2 5 2 x 2 x 2 x 2 x 2 32. Dengan menggunakan definisi tersebut kamu dapat mengubah bilangan berpangkat bulat negatif ke dalam bilangan bulat positif dan sebaliknya.
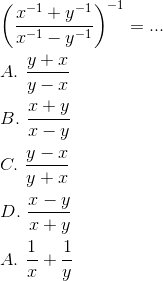
Rumus Rumus Pangkat
Contoh soal bilangan pangkat negatif. Contoh soal pangkat bulat negatif sifat sifat operasi bilangan berpangkat positif berlaku juga untuk bilangan berpangkat negatif dengan a b bilangan real dan m n bilangan bulat negatif. Berikut ini merupakan contoh soal pada penjelasan di atas agar kaju dapat lebih memahami materi yang disampaikan secara lebih mendalam. Didalam bilangan eksponen atau bilangan pangkat tidak selamanya selalu memiliki nilai bulat positif tetapi bisa juga bernilai nol negatif maupun pecahan. Selanjutnya coba kerjakan contoh soal dengan menggunakan sifat sifat bilangan berpangkat positif di bawah ini. 3 1 7 1 128 1 y 1. Meskipun soal ini menyediakan bilangan berpangkat bulat negatif jangan terkecoh dan menyulitkan dirimu sendiri dengan menjadikan seluruh pembilang dan penyebutnya ke dalam bentuk pecahan di dalam pecahan.
7 2 7 x 7 49. Sebagaimana yang kita ketahui bahwasannya eksponen atau pangkat biasanya yang tercantum yaitu bilangan asli atau bilangan bulat. Pangkat nol adalah a bilangan real dan juga a 0 sehingga a⁰ 1. Contoh soal bilangan berpangkat berbicara mengenai bilangan berpangkat tentu kalian sudah tidak asing lagi karena ini merupakan materi kelanjutan dari materi bilangan bulat yang telah kita bahas sebelumnya. Sebelum kita membahas mengenai contoh soal bilangan berpangkat sebaiknya anda mengerti dulu apa itu pengertian bilangan berpangkat. Sederhanakanlah bilangan berpangkat berikut ini.
Kamu bisa lho menerapkan salah satu sifat bilangan berpangkat bulat positif pada operasi perkalian yang ada di dalam soal ini. A bilangan dasar bilangan pokok n pangkat eksponen contoh. Bilangan berpangkat bulat positif. Berikut ini adalah pembahasan tentang bilangan bepangkat yang meliputi sifat sifat bilangan berpangkat operasi bilangan berpangkat contoh soal bilangan berpangkat contoh operasi bilangan berpangkat sifat sifat perpangkatan perkalian bilangan berpangkat pembagian bilangan berpangkat penjumlahan bilangan berpangkat pengurangan bilangan berpangkat perpangkatan bilangan berpangkat. Tidak semua bilangan berpangkat bernilai positif beberapa pangkat adalah bilangan bulat negatif. Pada pangkat nol bilangan a tidak boleh sama dengan nol karena pada saat a 0 maka a⁰ 0⁰ sehingga di dapatkan hasil yang tidak tentu.
Apabila m dan n merupakan bilangan bulat. X n sebanyak n ket. Apabila dirumuskan adalah. Rumuscoid setelah sebelumnya kita membahas tentang bilangan prima kali ini kita akan membahas materi tentang rumus bilangan positif dan negatif kita akan jabarkan secara detail dan lengkap mulai dari pengertian dan contoh bilangan positif negatif beserta pembahasannya. Bilangan berpangkat pecahan pengertian sifat rumus contoh soal dipembahasan sebelumnya kita sudah membahas materi mengenai bilangan berpangkat dan bilangan pecahan sekarang kita akan membahas materi bilangan berpangkat pecahan. Bilangan eksponen nol 0 apabila a 0 maka a 1 atau a tidak boleh sama dengan 0.
Yaitu merupakan penyederhanaan dari seatu perkalian bilangan bulat yang memiliki faktor yang sama. A n a x a x a x a x.